Offline Imitation from Observation via Primal Wasserstein State Occupancy Matching
Kai Yan, Alexander G. Schwing, Yu-Xiong Wang
ICML, 2024
Vienna, Austria
PDF | Code | Poster | Slide | Bibtex
Abstract
Distance metric matters for imitation based on Wasserstein distance;
we provide both flexibility and good choice on this.
Full Abstract
In real-world scenarios, arbitrary interactions with the environment can often be costly, and actions of expert demonstrations are not always available. To reduce the need for both, offline Learning from Observations (LfO) is extensively studied: the agent learns to solve a task given only expert states and *task-agnostic* non-expert state-action pairs. The state-of-the-art DIstribution Correction Estimation (DICE) methods, as exemplified by SMODICE, minimize the state occupancy divergence between the learner's and empirical expert policies. However, such methods are limited to either $f$-divergences (KL and $\chi^2$) or Wasserstein distance with Rubinstein duality, the latter of which constrains the underlying distance metric crucial to the performance of Wasserstein-based solutions. To enable more flexible distance metrics, we propose Primal Wasserstein DICE (PW-DICE). It minimizes the primal Wasserstein distance between the learner and expert state occupancies and leverages a contrastively learned distance metric. Theoretically, our framework is a generalization of SMODICE, and is the first work that unifies f-divergence and Wasserstein minimization. Empirically, we find that PW-DICE improves upon several state-of-the-art methods. The code is available at https://github.com/KaiYan289/PW-DICE.How Does Distance Metric Matter?
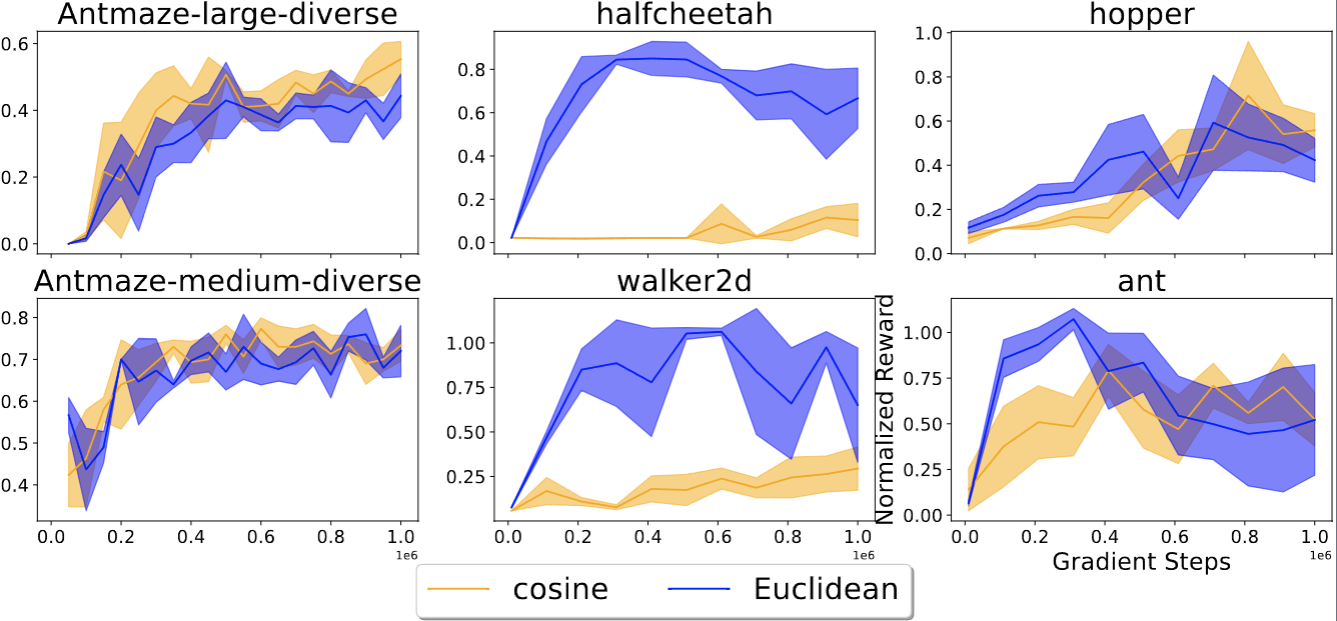
We test OTR [1] on the D4RL MuJoCo dataset with testbeds appearing in both SMODICE [2] and OTR [1]. We found that there are significant performance difference between cosine-similarity-based occupancy used by OTR and Euclidean distance, which means selecting a good metric is crucial for the performance of Wasserstein-based solutions.
What is Our Solution?
The following figure shows a comparison between our proposed solution and existing methods, where gray shows suboptimal design:
| — | Geometric property of distributions | Distance metric | Matching Objects | Optimizing objective itself |
|---|---|---|---|---|
| f-divergence-based methods [2, 4] | No | KL or chi-square | Distributions | Yes |
| Wasserstein-based methods with Rubinstein duality [5] | Yes | Euclidean | Distributions | Yes |
| PWIL [3] | Yes | (Standardized) Euclidean, potentially flexible | Distributions | No (optimizing upper-bound) |
| OTR [1] | Yes | (Normalized) Cosine, potentially flexible | States | Yes |
| Our method | Yes | Flexible, Learned | Distributions | Yes |
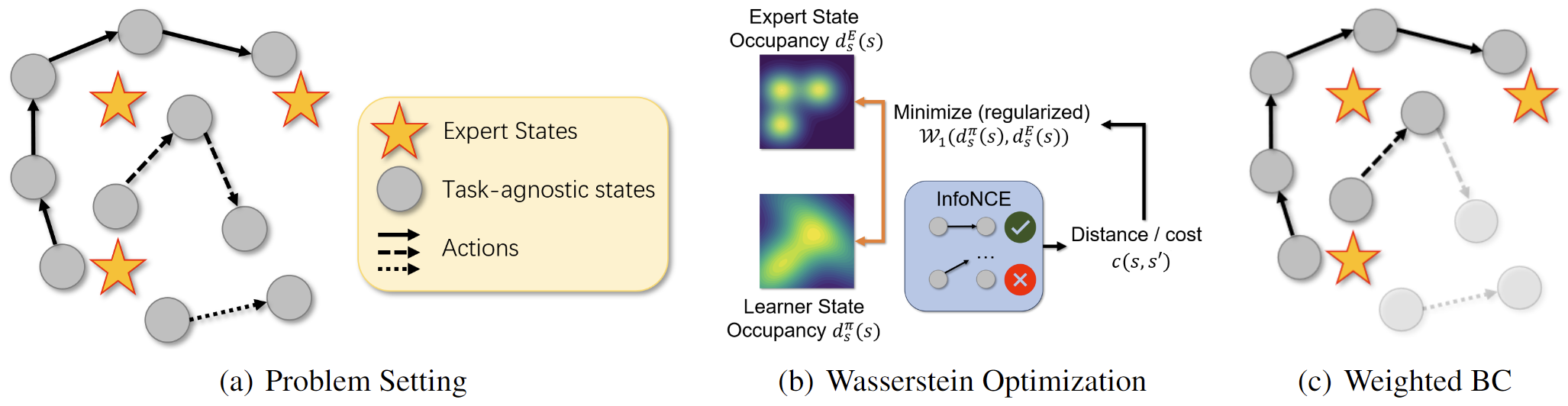
We learn offline from expert states and non-expert (task-agnostic) transitions. We choose primal Wasserstein distance with a KL regularizer that minimizes state occupancy between the learner’s policy and the expert policy.
-
Primal Wasserstein distance allows for flexible distance metric, for which we use a distance combined from contrastive learning in InfoNCE [6] and discriminator scores from SMODICE [2] that reflects the reachability between states in the dataset;
-
KL regularizer helps us to remove the constraints in its dual problem. Specially, we prove that SMODICE is a special case of our solution with particular choice of KL regularizers.
-
We solve a single-level convex optimization in dual space, and use the solved dual variable as weight for weighted behavior cloning the offline, less related, task-agnostic dataset.
Performance
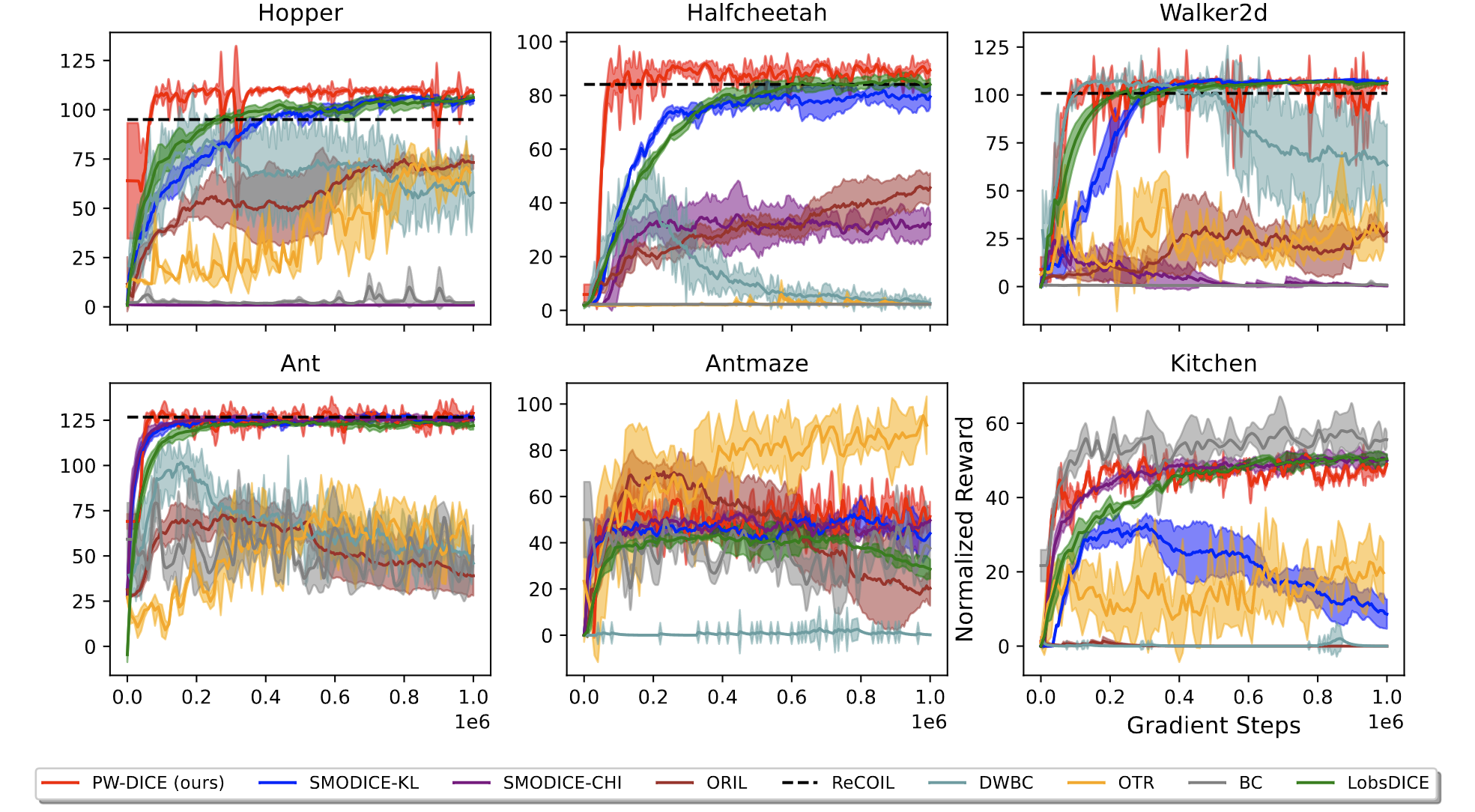
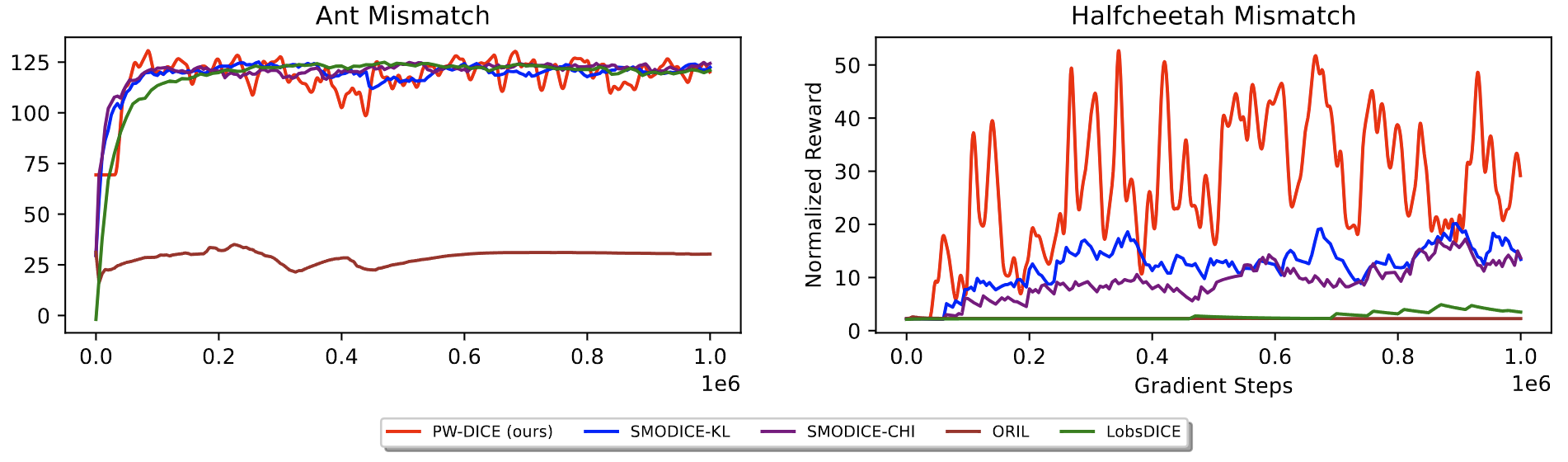
We test our methods on multiple scenarios, including tabular MDPs [3] and D4RL [7] environments. Our learned embedding brings adjacent states apart in Euclidean space together in the embedding (as shown below), and is more robust than baselines with distorted state representations and expert data with different dynamics. See our paper for experiment details.
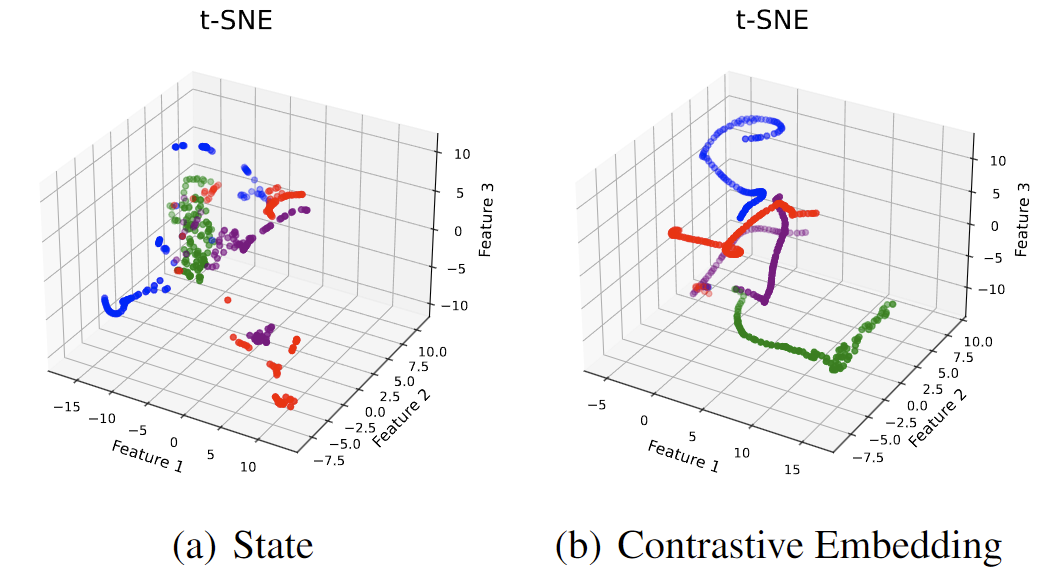
t-SNE results of states from different trajectories before (a) and after (b) embedding.
Tabular MDPs
Regret (Lower is Better)
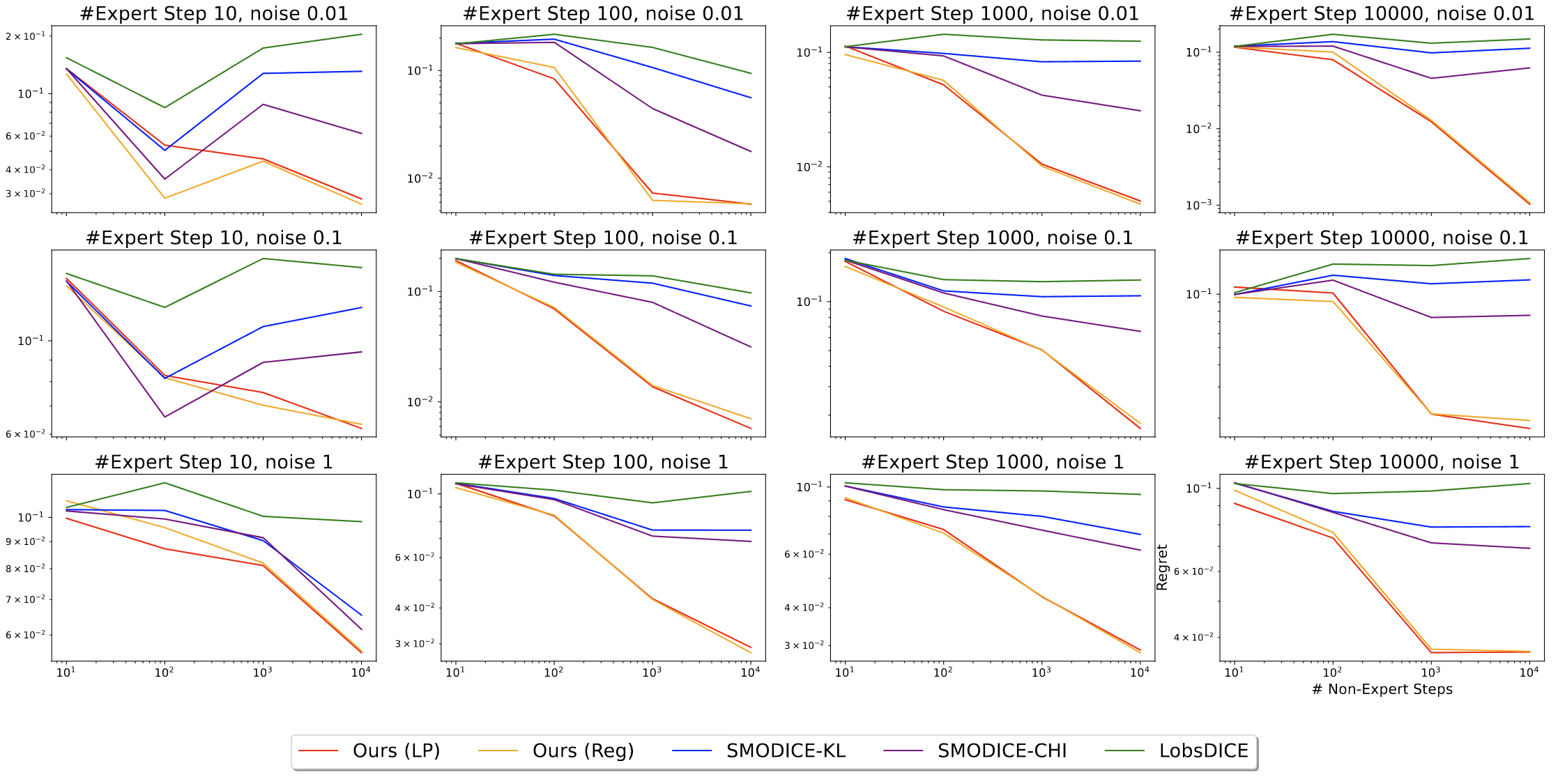
TV distance between state occupancies (Lower is Better)
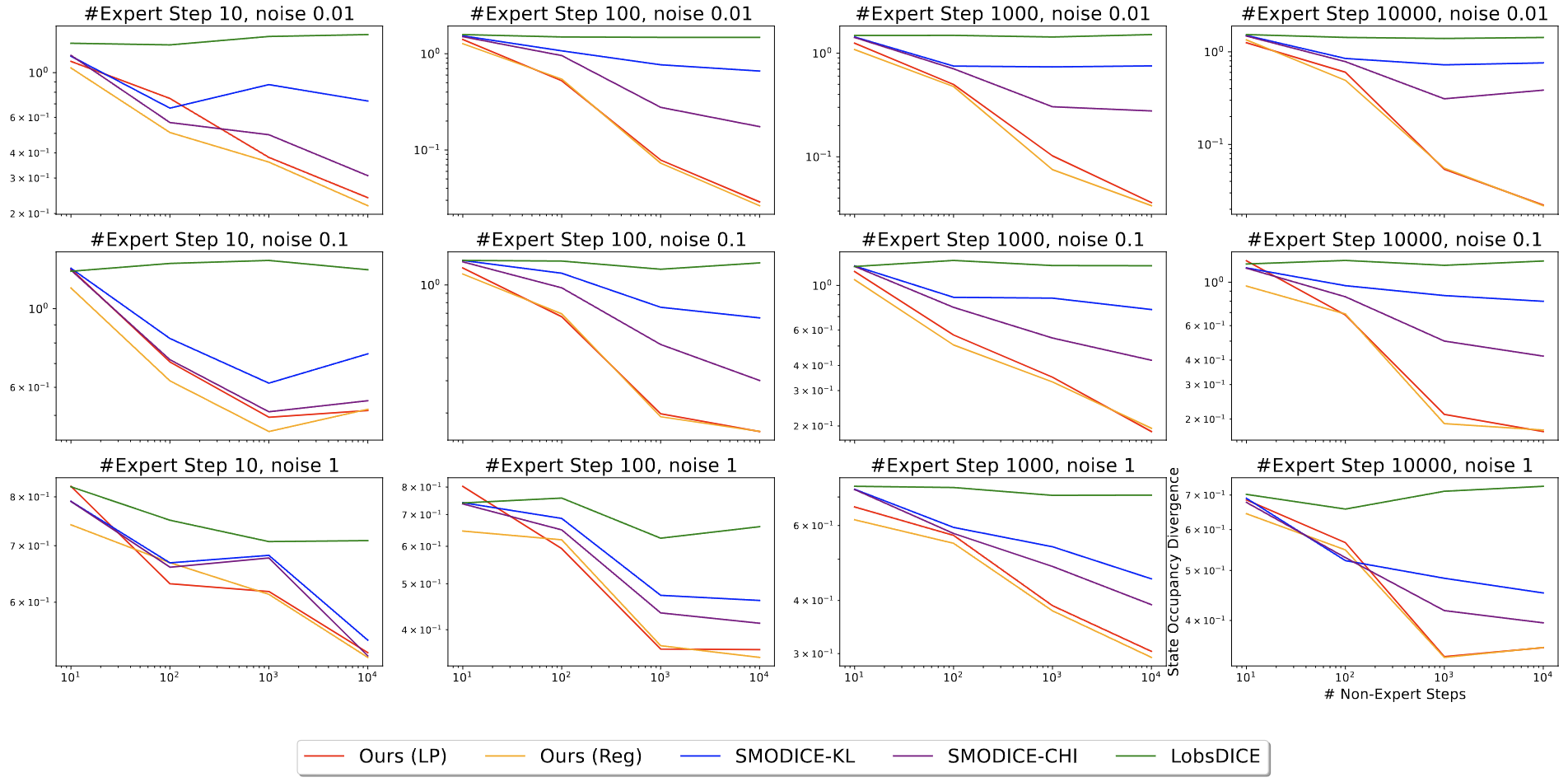
TV distance between state-pair occupancies (Lower is Better)
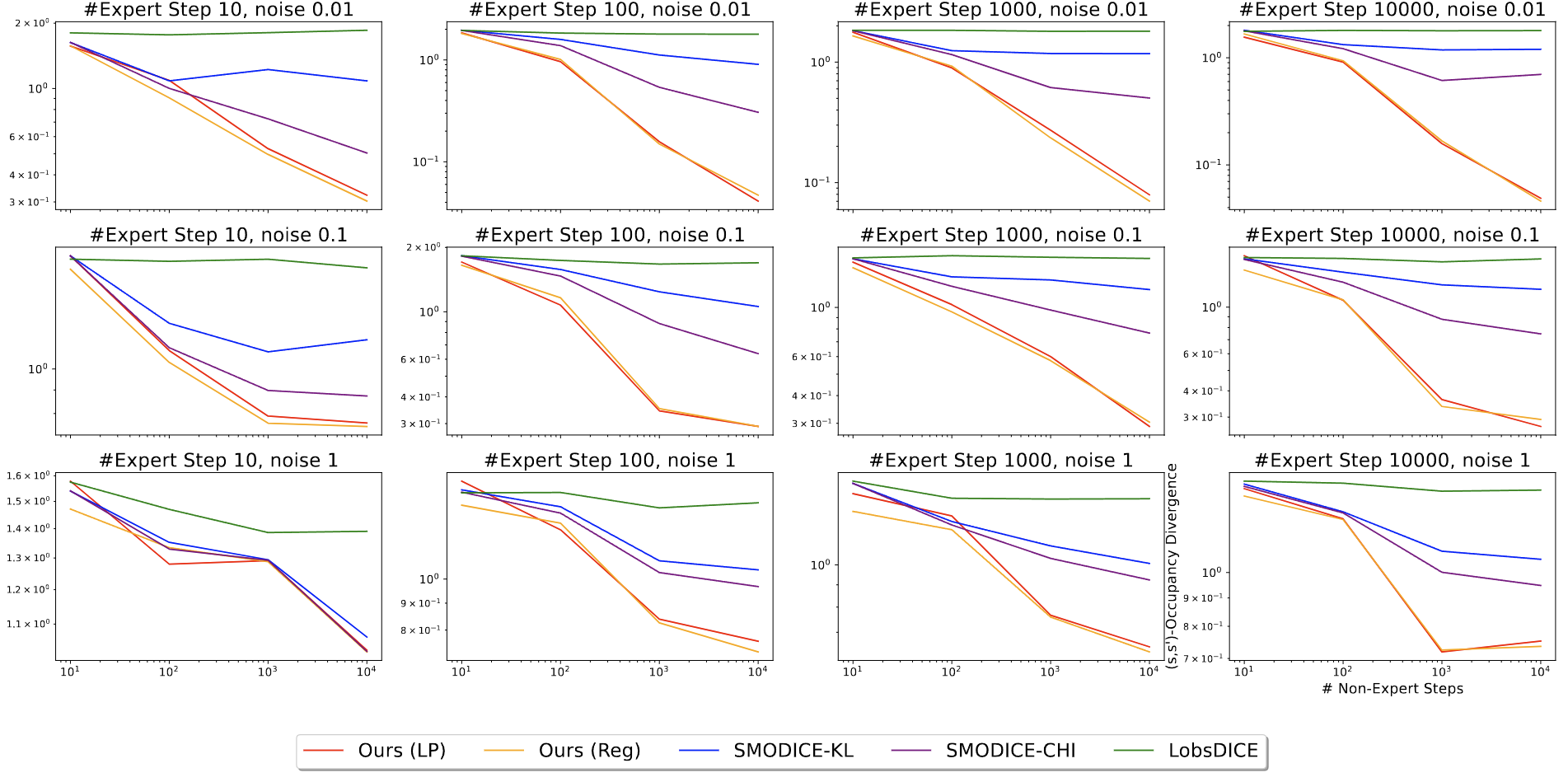
D4RL Environments
Normalized Rewards (Higher is Better)
Distorted State Representations
Normalized Rewards (Higher is Better)
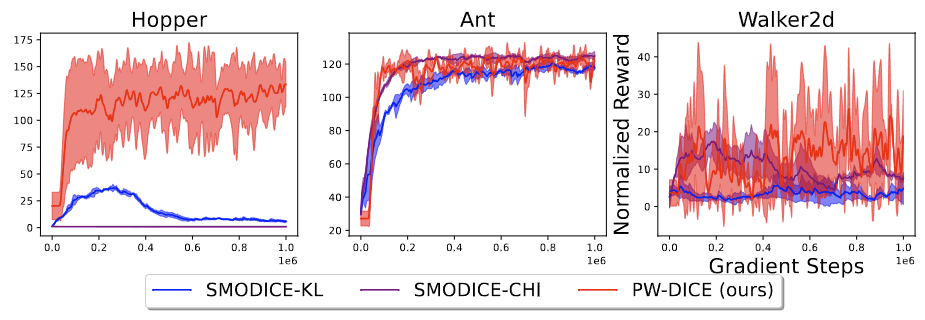
Expert Data with Different Dynamics
Normalized Rewards (Higher is Better)
Related Work
[1] Y. Luo, Z. Jiang, S. Cohen, E. Grefenstette, and M. P. Deisenroth. Optimal transport for offline imitation learning. In ICLR, 2023.
[2] Y. J. Ma, A. Shen, D. Jayaraman, and O. Bastani. Smodice: Versatile offline imitation learning via state occupancy matching. In ICML, 2022.
[3] R. Dadashi et al. Primal wasserstein imitation learning. In ICLR, 2021.
[4] G. hyeong Kim, J. Lee, Y. Jang, H. Yang, and K. Kim. Lobsdice: Offline learning from observation via stationary distribution correction estimation. In NeurIPS, 2022.
[5] H. Xiao, M. Herman, J. Wagner, S. Ziesche, J. Etesami, and T. Hong Linh. Wasserstein Adversarial Imitation Learning. ArXiv, 2019.
[6] A. Oord, Y. Li, and O. Vinyals. Representation Learning with Contrastive Predictive Coding. ArXiv, 2018.
[7] J. Fu, A. Kumar, O. Nachum, G. Tucker and S. Levine. D4RL: Datasets for Deep Data-Driven Reinforcement Learning. ArXiv, 2020.